Le paradoxe exposé par le sociologue Jerry Harvey concerne la relation à la prise de décision au sein d'un groupe.

Le paradoxe d’Abilene, présenté dans son ouvrage The Abilene Paradox and Other Meditations on Management (San Francisco : Jossey-Bass, 1988) est une illustration de la difficulté d’un groupe à prendre une décision et gérer collectivement son accord.

Dans la fable moderne que propose Jerry B. Harvey, aucun des 4 membres d'un groupe ne souhaitait se rendre à Abilene mais par crainte de s’offenser et de se contredire mutuellement, ils y finissent tous !

L'histoire

"Quatre adultes, un couple marié et les parents de la femme, sont assis sous un porche dans une chaleur abrutissante dans la petite ville de Coleman, au Texas, à environ 53 miles d'Abilene. Ils sirotent tristement de la citronnade, observant le ventilateur souffreteux et entamant de temps à autre une partie de domino. À un moment, le père de l’épouse suggère qu'ils se rendent à Abilene pour se restaurer dans une cafétéria. Le gendre pense que c'est une idée folle mais n’ose pas contrarier sa femme qui voit si peu ses parents. Les deux femmes ne semblent pas opposées à cette idée et voilà tout ce petit monde entassé dans une Buick sans air climatisé, qui soulève sur le chemin des nuages de poussière. À Abilene, ils mangent un déjeuner médiocre dans un endroit glauque et reviennent à Coleman épuisés, suants, et peu satisfaits du périple. C’est une fois de retour à la maison qu’ils se rendent comptent qu'aucun d'eux n'avait vraiment voulu aller à Abilene. Le beau-père l’avait proposé et les autres l’avaient accepté juste parce que chacun avait pensé intérieurement, sans le vérifier, que les autres étaient désireux d'y aller."

Cette anecdote sert de base à des enseignements sur les dynamiques de groupe, ainsi que sur le management décisionnel. La principale leçon à en tirer est que dans certaines conditions, un groupe non structuré peut entériner des décisions par consensus alors qu'en fait, aucun des participants ne soutenait la proposition initiale (et aucun n'aurait voté par bulletins secrets).

Source : Wikipédia [Fr]

Le problème de Monty Hall est un casse-tête probabiliste librement inspiré du jeu télévisé américain Let's Make a Deal. Il est simple dans son énoncé mais non intuitif dans sa résolution et c'est pourquoi on parle parfois à son sujet de paradoxe de Monty Hall. Il porte le nom de celui qui a présenté ce jeu aux États-Unis pendant treize ans, Monty Hall.

Énoncé

Le jeu oppose un présentateur à un candidat (le joueur). Ce joueur est placé devant trois portes fermées. Derrière l'une d'elles se trouve une voiture (ou tout autre prix magnifique) et derrière chacune des deux autres se trouve une chèvre (ou tout autre prix sans importance). Il doit tout d'abord désigner une porte. Puis le présentateur ouvre une porte qui n'est ni celle choisie par le candidat, ni celle cachant la voiture (le présentateur sait quelle est la bonne porte dès le début). Le candidat a alors le droit ou bien d'ouvrir la porte qu'il a choisie initialement, ou bien d'ouvrir la troisième porte.

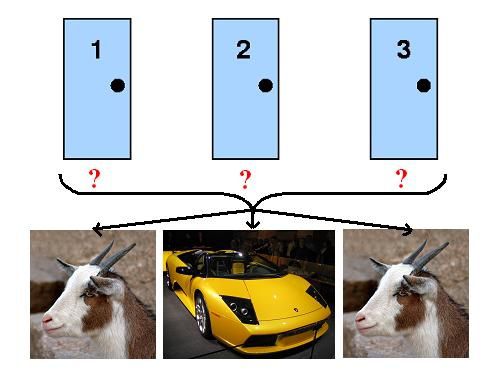
Les données de base du problème de Monty Hall : Soient trois portes cachant soit une chèvre soit une superbe voiture, l'automobile étant derrière une seule porte et deux chèvres se cachant derrière les deux autres portes.

Les questions qui se posent au candidat sont :

1. - Que doit-il faire ?
2. - Quelles sont ses chances de gagner la voiture en agissant au mieux ?

Historique et évolution de l'énoncé du problème

Ci-dessous est reproduite la traduction d'un énoncé célèbre du problème, issu d'une lettre que Craig F. Whitaker avait fait paraître dans la rubrique Ask Marylin de Marilyn vos Savant du Parade Magazine en septembre 1990 :

 

« Supposez que vous êtes sur le plateau d'un jeu télévisé, face à trois portes et que vous devez choisir d'en ouvrir une seule, en sachant que derrière l'une d'elles se trouve une voiture et derrière les deux autres des chèvres. Vous choisissez une porte, disons la numéro 1, et le présentateur, qui lui sait ce qu'il y a derrière chaque porte, ouvre une autre porte, disons la numéro 3, porte qui une fois ouverte découvre une chèvre. Il vous demande alors : « désirez-vous ouvrir la porte numéro 2 ? ». À votre avis, est-ce à votre avantage de changer de choix et d'ouvrir la porte 2 plutôt que la porte 1 initialement choisie ? »

La publication de cet article dans le Parade Magazine a eu un impact immédiat sur le lectorat et a engendré de très nombreuses discussions parmi les mathématiciens, célèbres ou non, et les amateurs anonymes. Marilyn vos Savant, réputée pour figurer au Guinness Book of Records comme étant la personne au quotient intellectuel le plus élevé au monde (QI de 228), a ainsi reçu plus de 10 000 lettres (estimation faite par elle-même) traitant du problème, dont plusieurs provenant d'universitaires remettant en question la pertinence de la démonstration reproduite dans sa rubrique. En 1991, pour une édition dominicale, la une du New York Times ouvre sur ce sujet. Jerry Pournelle, célèbre chroniqueur du Chaos Manor de Byte, a également discuté le problème longuement en tant qu'adversaire de la solution de Marilyn, pour se ranger finalement de son côté. Enfin, une discussion controversée a eu lieu à propos de l'article du Parade Magazine dans la rubrique The Straight Dope tenue par Cecil Adams dans l'hebdomadaire The Chicago Reader.

La pertinence des résultats statistiques était parfois contestée, mais ce qui posait le plus souvent problème était que l'article n'insistait pas sur les « contraintes » du présentateur. Les résultats donnés impliquaient nécessairement les postulats suivants :

• Que le présentateur ne peut ouvrir la porte choisie par le candidat.
• Que le présentateur donne systématiquement la possibilité au candidat de revenir sur son choix initial.

Or, comme ces éléments n'étaient pas mis en avant dans l'énoncé du problème, et ce même s'ils étaient implicites, d'autres résultats statistiques que ceux donnés dans l'article devenaient possibles. Rien n'indiquant que l'énoncé de départ doive nécessairement inclure ces postulats, on devrait pouvoir généraliser le problème à d'autres cas.

Finalement, en considérant que ces postulats étaient une condition sine qua non de l'énoncé du problème, il s'est avéré que les résultats de l'article étaient effectivement justifiés.

Cependant il manquait au moins un élément de taille : la question de savoir si le candidat devait ou non changer sa décision initiale pour avoir plus de chances de gagner la voiture n'avait de sens que si l'énoncé précisait bien que le présentateur savait précisément ce qui se cachait derrière chaque porte, élément justement omis dans l'article du Parade Magazine. Si le présentateur ne le savait pas, alors la question aurait été dénuée de sens.

Cela dit, cet énoncé ne fait que s'inscrire dans la lignée de ceux consacrés à ce type de paradoxe.

En effet, une des premières apparitions de ce problème date de 1898 dans Probabilités de Calcul de Joseph Bertrand où il est décrit comme le paradoxe de la boîte de Bertrand.

Un énoncé actuel exempt d'ambiguïté

Il est donc préférable de se baser sur un énoncé non équivoque du problème, incluant donc expressément les contraintes du présentateur, décrit par Mueser et Granberg comme suit :

• Derrière chacune des trois portes se trouve soit une chèvre, soit une voiture, mais une seule porte donne sur une voiture alors que deux portes donnent sur une chèvre. La porte cachant la voiture a été choisie par tirage au sort.
• Le joueur choisit une des portes, sans que toutefois ce qui se cache derrière (chèvre ou voiture) ne soit révélé à ce stade.
• Le présentateur sait ce qu'il y a derrière chaque porte.
• Le présentateur doit ouvrir l'une des deux portes restantes et doit proposer au candidat la possibilité de changer de choix quant à la porte à ouvrir définitivement.
• Le présentateur ouvrira toujours une porte derrière laquelle se cache une chèvre, en effet :
  • Si le joueur choisit une porte derrière laquelle se trouve une chèvre, le présentateur ouvrira l'autre porte où il sait que se trouve également une chèvre.
  • Et si le joueur choisit la porte cachant la voiture, le présentateur choisit au hasard parmi les deux portes cachant une chèvre. (on peut supposer qu'un tirage au sort avant l'émission a décidé si ce serait la plus à droite ou à gauche)
• Le présentateur doit offrir la possibilité au candidat de rester sur son choix initial ou bien de revenir dessus et d'ouvrir la porte qui n'a été choisie ni par lui-même, ni par le candidat.

La question qui se pose alors est :

• Le joueur augmente-t-il ses chances de gagner la voiture en changeant son choix initial ?

Ou formulé autrement, cela revient à dire :

• Est-ce que la probabilité de gagner en changeant de porte est plus grande que la probabilité de gagner sans changer de porte ?

Ou encore :

• Quelle est la meilleure stratégie : Faire un nouveau choix ou rester avec le choix initial ? Les chances de gain vont-elles augmenter, diminuer ou bien resteront-elles les mêmes ?

Clés pour comprendre le problème

Raisonnement par la probabilité que le présentateur apporte de l'information

Prenons le cas d’un candidat qui suit toujours la même stratégie à chaque jeu, celle de maintenir systématiquement son premier choix. Ce candidat aura donc 1 chance sur 3 de gagner la voiture. En moyenne, il gagnera donc une fois sur trois et perdra forcement 2 fois sur 3, exactement comme si le présentateur n'ouvrait pas de porte.

Au contraire, un candidat qui suit la stratégie inverse, changer systématiquement son premier choix, gagnera en moyenne 2 fois sur 3, en effet, lorsque le présentateur ouvre une porte deux cas de figure sont possibles:

• Soit le candidat avait choisi la voiture (1 chance sur 3) et le présentateur ouvre n'importe quelle porte, n'apportant pas d'information,
• Soit le candidat avait choisi une chèvre (2 chances sur 3) et le présentateur ouvre la porte de la seule chèvre restante, désignant de fait la porte restante comme celle cachant la voiture.

Donc faire confiance au présentateur en changeant son choix apporte 2 chances sur 3 de gagner.

On note au passage que le présentateur n'a absolument aucune liberté dans le fait d'apporter de l'information ou non, donc que sa volonté d'aider ou de nuire n'a aucun effet.

Raisonnement par les probabilités complémentaires

Lorsque le candidat choisi une porte, il y a 1 chance sur 3 que ce soit celle de la voiture, et 2 chances sur 3 qu'il y ait une chèvre derrière. Ces probabilités sont des probabilités a priori et ne changeront donc jamais pendant toute la durée du jeu. Lorsque le présentateur fait sortir une chèvre, la probabilité d'avoir une chèvre derrière la porte choisie est toujours de 2/3, et donc la probabilité que la voiture soit derrière la porte restante est également de 2/3. D'où l'intérêt pour le candidat de choisir la porte restante et de changer son choix.

Diagramme servant à faciliter l'explication.

Source : Wikipédia - Problème de Monty Hall [Fr]

Voir aussi : Le paradoxe des (trois) prisonniers

Dans la tradition judéo-chrétienne, le mythe de la Tour de Babel conte que Nemrod, descendant de Noé, voulut édifier une grande tour qui devait atteindre le ciel.

Mais Dieu, estimant cette entreprise par trop orgueilleuse, décida de contrecarrer le projet en multipliant les langues parlées à Babylone, de telle sorte que plus personne, sur le chantier, ne puisse se comprendre, et qu'ainsi, l'édification de la grande ziggourat soit abandonnée.

L'interprétation de ce mythe allégorique, comme toute histoire symbolique, revêt différents aspects. L'une de ces interprétations est que pour atteindre "le ciel", c'est-à-dire Dieu (ou l'état divin, faisant de l'Homme l'égal de Dieu) il est nécessaire que tous les Hommes se comprennent et s'entendent. Sans cet entendement et cette compréhension mutuelle, les humains sont condamnés à rester divisés, et ils ne peuvent s'élever.

Source : Agoravox.fr

Le système politique est un mode d'organisation d'un État. Le système politique comprend notamment le régime politique, la structure économique, l'organisation sociale, etc.

Les systèmes politiques sont nombreux. On y retrouve notamment la démocratie, le monarchisme, le féodalisme, le totalitarisme, l'autoritarisme, etc.

Les types de systèmes politiques

Les systèmes politiques existants ou proposés sont multiples. Il est habituel de les classer entre régimes démocratiques et régimes autoritaires, mais dans la pratique la situation n'est pas toujours aussi tranchée.

Platon distingue cinq systèmes politiques correspondant à cinq formes d'âmes humaines. "S'il y a cinq formes de constitution, il doit y avoir aussi chez les particuliers cinq formes d'âme (La République, 544e). Les cinq sont : monarchie (aristocratie), timocratie (recherche des honneurs), oligarchie (recherche des richesses), démocratie, tyrannie (violence).

Système démocratique

La démocratie est un système caractérisé par l'appartenance du pouvoir par le peuple. Sur le plan international, la démocratie est considéré comme le système idéal à atteindre.

Exemples de régime politique démocratique

• -Régime parlementaire
• -Régime présidentiel
• -Régime d'assemblée
• -Fédéralisme

Système totalitaire

Le totalitarisme est un régime à parti unique, n'admettant aucune opposition organisée, dans lequel l'État tend à confisquer la totalité des activités de la société. . Ce système est caractérisé par :

• -L'autorisation de l'existence d'un seul parti (Parti Unique) contrôlant l'Etat, dirigé idéalement par un chef charismatique
• -La présence d'une idéologie imposée
• -Un contrôle de la population allant jusqu'à remettre en cause la liberté de penser
• -Un monopole des moyens de communications et des forces armées
• -Un recours à la terreur

Exemples de régimes politiques totalitaires

Plusieurs régimes à travers l'histoire ont eu des éléments totalitaristes. On peut considérer l'URSS communiste, comme un système totalitaire, tandis que plusieurs auteurs limitent cette notion à la période staliniste.

On retrouve plusieurs exemples à travers le temps de régime politique totalitaire :

• -Stalinisme
• -Le Troisième Reich

Système autocratique

Les systèmes autoritaires sont, tout comme les systèmes totalitaires, des organisations arbitraires de la société qui ne laissent pas de place à la société civile. Par contre, si dans un système totalitaire on assiste à une fusion de la sphère publique et de la sphère privée, les systèmes autoritaires sont caractérisés par une exclusion des citoyens à la participation publique.

Bien que l'élement de la violence ne soit pas une composante systématique dans les systèmes autocratiques, souvent les deux vont de pairs.

Exemples de régimes politiques autoritaires

• -Dictature
• -Dictature militaire
• -Oligarchie raciale

À travers l'histoire, on pourrait retenir entre autres le Premier Empire Français de Napoléon I^er, ou la République sociale italienne de Benito Mussolini.

Système théocratique

La Théocratie est un système politique où la légitimité politique découle de la divinité. La souveraineté y est exercée par la classe sacerdotale, qui cumule pouvoir temporel et religieux.

Système féodal

La féodalité est un système politique dont l'autorité centrale a été affaiblie ; le pouvoir souverain est attribué à des principautés, des fiefs ou des fédérations gouvernés par des seigneurs et destinés à stabiliser la région et/ou le peuple.

Cette organisation de la société se développa en Europe entre le cinquième et le huitième siècle, après le démembrement de l'Empire romain d'Occident. Basée sur le droit romain et le système dit de « l'hospitalité », la féodalité est propre à l'Occident européen.

Système monarchique

Le monarchisme est une doctrine politique qui prône la monarchie, c’est-à-dire une forme de gouvernement dans laquelle l'État est dirigé par une seule personne qui représente ou exerce l'ensemble des pouvoirs. On peut distinguer plusieurs monarchismes :

• -La monarchie de droit divin : par exemple l'Ancien Régime
• -La monarchie absolue : encore présente entre autres en Arabie saoudite
• -La monarchie constitutionnelle et la monarchie parlementaire : le Royaume-Uni, la Belgique, le Canada ...

Systèmes composites ou intermédiaires

• -Corporatisme, doctrine économique et sociale basée sur le regroupement de différents corps de métier au sein d'institutions défendant leurs intérêts.
• -Jacobinisme, doctrine politique qui défend la souveraineté populaire et l'indivisibilité de la République française. Il tient son nom du club des Jacobins parisien où ses membres, issus du mouvement du jansénisme parlementaire, s'étaient établis pendant la Révolution française, dans l'ancien couvent des Jacobins.

Source : Wikipédia - Système politique [Fr]

Des scientifiques ont fait une découverte importante : ils ont découvert quelle partie du cerveau fait que l'on se conforme aux attentes du groupe et à sa « pression ».

Mieux : les chercheurs peuvent ainsi arriver à contrôler ce conformisme auprès de volontaires en utilisant de puissantes impulsions électromagnétiques. Ces impulsions permettent donc de modifier l'activité dans la petite région du cerveau concernée.

On pense que cette partie du cerveau provient de notre lointaine évolution : elle est là pour corriger nos actions lorsqu'on n'est plus « en phase » avec le groupe.

Les expériences ont pu montrer au passage que certains individus sont plus conformistes que d'autres.

Suspendre ce mécanisme permet de penser et d'agir différemment. On pourrait donc tout à fait développer des médicaments ou des techniques de modifications comportementales afin d'accroître ou décroître le conformisme chez les gens.

On peut également doser notre dopamine interne pour modifier notre conformisme, mais l'usage est controversé, car des sociétés pourraient s'en servir pour n'avoir que des employés modèles...

Source : Sur-la-toile